How to help a daughter with Pre-Algebra, with a $5000 Mathematica seat

Image via Wikipedia

(Actually, you will pay less for Mathematica than I do.  I believe you will pay $200)

Here is a session in Mathematica's Notebook REPL (Read-eval-print-loop).  If you are simply performing an operation on the last bit of output, simply type "%".  Remember, "Solve" works on equations, and inequalities require the use of "Reduce".  In "Reduce", don't be thrown by Mathematica taking care to note the domain of the variables.  "Expand" can force Mathematica to carry out all the productions in the expression.  "MapAt" is great to change just one part of an expression.  "Remove["Global`*"];" is how you can just re-evaluate a whole Notebook from scratch, and not have to worry about conflicts with earlier assignments as you were exploring different implementations and techniques.  "RegionPlot" is just the thing for viewing inequalities.

In:= Remove["Global`*"];

In:= slope[{x0_,y0_},{x1_,y1_}]:=(y1-y0)/(x1-x0)

In:= slope[{-6,3},{2,-5}]
Out= -1

In:= slope[{1,3},{-2,-1}]
Out= 4/3

In:= Solve[{-3x-y==2,-4x+2y==8},{x,y}]
Out= {{x->-(6/5),y->8/5}}
In:= N[%]
Out= {{x->-1.2,y->1.6}}

In:= Solve[-3x-y==2,{y}]
Out= {{y->-2-3 x}}

In:= Solve[-4x+2y==8,{y}]
Out= {{y->2 (2+x)}}
In:= MapAt[Expand[#]&,%,{1,1}]
Out= {{y->4+2 x}}

In:= Solve[{y-x==3,2x+y==-2},{x,y}]
Out= {{x->-(5/3),y->4/3}}
In:= N[%]
Out= {{x->-1.66667,y->1.33333}}
In:= Reduce[y-x<=3,{y}]
Out= x\[Element]Reals&&y<=3+x
In:= Reduce[2x+y<-2,{y}]
Out= x\[Element]Reals&&y<-2-2 x

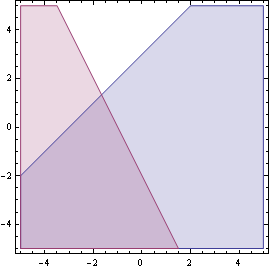
In:= RegionPlot[{y-x<=3,2x+y<-2},{x,-5,5},{y,-5,5}]
Out=

For some stupid reason, I alway forget "Rise Over Run" for the slope.  So now I can just cut and paste.